Chan vektoryèl



Nan matematik, yon chan vektoryèl oswa chan vektè se yon fonksyon ki asosye yon vektè ak chak pwen nan ' yon espas Euclidean oswa plis jeneralman nan yon manifoul diferansyèl[1]. Pou rezolisyon ekwasyon diferansye otonòm 1e lòd, nou itilize chan direksyon (ki rele nan jaden vitès fizik) ki reprezante dérivés tanjant nan trajectoire ekwasyon sa yo, ki pèmèt yo trase li.
Souvan yo itilize jaden vektè nan fizik, pou egzanplè vitès ak direksyon yon likid k ap deplase nan espas, oswa valè ak direksyon yon fòs, tankou fòs mayetik la. oswa gravitasyonèl, ki evolye soti nan yon pwen rive nan pwen vwazen li.
Konsèp matematik
[modifye | modifye kòd]Se pou E yon espas vektè eklidyen ak U se yon louvri nan E. Yon jaden vektè klas regilarite sou U se yon kat F nan klas U nan E, defini pa fonksyon eleman n li yo:
Egzanp:
Jaden gradyan
[modifye | modifye kòd]Yon jaden vektè X yo rele yon champ gradyan[2] lè gen yon fonksyon f tankou nan nenpòt ki pwen, X se gradyan nan f. Nou toujou di ke X soti nan potansyèl f. Nan ka sa a, diferan potansyèl yo diferan pa yon konstan.
Nan plan an, si jaden vektè X la soti nan yon potansyèl f, liy nivo f, koub sou ki f egal. a yon konstan, yo rele koub ekipotential pou jaden vektè a. Nan nenpòt ki pwen kote jaden an pa zewo, li nòmal pou koub ekipotensyal yo.
Si jaden vektè a trase sou yon espas ouvè ki gen twa dimansyon, nou pale tou de sifas ekipotansyèl. Plis jeneralman, nan nenpòt dimansyon, nou ap fè fas ak hypersurfaces ekipotansyèl, kote jaden vektè a nòmal.
Nan espas ki genyen twa dimansyon, yon jaden gradyan toujou gen zewo wotasyonèl. Kontrèman an enplike topoloji nan U louvri: si U se senpleman konekte, yon jaden vektè se yon jaden gradyan si epi sèlman si wotasyon li se nil.
Sikilasyon sou yon chemen
[modifye | modifye kòd]Yo itilize nosyon sikilasyon an patikilye nan fizik pou kalkile travay yon fòs.
Se pou yon chemen trase sou U ki louvri, sa vle di yon parameterize arc [a,b] nan U, nan klas . Sikilasyon jaden vektè X ansanm se
vle di pwodwi pwen vektè u ak v.
Valè sa a pa chanje lè w chanje parametrizasyon.
Si jaden an sòti nan yon gradyan f, sikilasyon an depann sèlman de pwent chemen an
Sa a se patikilyèman ka a nan yon champ elektrik, paske li sòti nan potansyèl elektrik:
An patikilye, li se zewo sou tout Yaw (chemen fèmen).
Duality ak fòm diferans
[modifye | modifye kòd]Yon fòm diferansyèl degre yonn ak klas sou U se yon jaden fòm lineyè, sa vle di yon < math>\mathcal C^k</math> kat jeyografik U nan double espas E* nan E' '. Nosyon sa a gen yon relasyon solid ak sa ki nan jaden an vektè.
Vreman vre, espas ki eklidyen an, pwodwi eskalè pèmèt nou defini yon izomòfis ant E ak doub li yo. Si X se yon jaden vektè sou U, nou ka asosye li ak fòm diferans ki defini nan chak pwen pa
epi asosyasyon sa a se yon bijeksyon ant jaden vektè ak fòm diferans nan lòd 1.
An konsekans, analoji ki genyen ant teyorèm yo konsènan fòm diferans ak jaden vektè pa etone: isit la se yon tablo korespondans.
| Jaden vektè | Diferans fòm lòd 1 |
|---|---|
| Trafik | Entegral koubiline |
| Jaden gradyan | Fòm diferans egzak |
| Wotasyon (dim 3) | Derive ekstèn |
| Zero wotasyon (dim 3) | Fòm diferans fèmen |
Remak: nou ka pwolonje nosyon wotasyon an nan lòt dimansyon pase 3.
Koub entegral nan yon jaden vektè, liy jaden
[modifye | modifye kòd]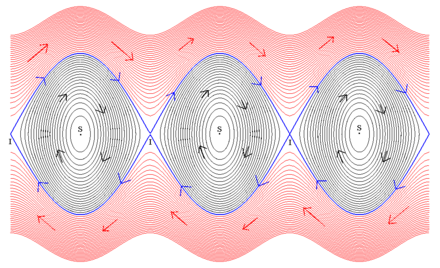
Nan jaden vektè X trase sou U ouvè a, nou ka asosye ekwasyon diferansyèl . Fonksyon solisyon yo se ark paramèt klas sou yon entèval I epi konsa ke
Sa vle di, vektè derive nan chak pwen bay nan jaden an nan pwen sa a.
Solisyon maksimòm ekwasyon diferans sa a rele "kob entegral" jaden vektè a[3]. Yo tanjant nan chak pwen nan jaden vektè a. Nan ka yon jaden gradyan, yo se poutèt sa orthogonal nan liy yo nivo oswa sifas yo. Fonksyon ki nan t, x asosye pwen ki te nan pozisyon x nan moman 0 yo rele koule diferans lan. ekwasyon.
Teyorèm Cauchy-Lipschitz asire egzistans ak inik yon solisyon maksimòm pou chak pè kondisyon inisyal (t0,x0) . Li ta aplike menm si jaden an te sèlman yon fonksyon Aplikasyon Lipschitzian.
Jaden vektè sou yon manifoul diferans
[modifye | modifye kòd]Dapre definisyon, yon jaden vektè sou yon manifoul diferansyèl se yon seksyon nan pakèt tanjant manifoul sa a.
Yo dekri yon jaden konsa nan vwazinaj chak pwen regilye li yo, pa teyorèm rektifikasyon an: gen yon kat lokal kote yo li jaden an kòm "premye vektè kowòdone".
Si varyete nan kontra enfòmèl ant, liy jaden yo mete sou nonb antye relatif ℝ.
Aplikasyon nan fizik vag
[modifye | modifye kòd]Yon ekwasyon diferansyèl ki gen jaden vektè kòm solisyon (ki reprezante, pa egzanp, pwopagasyon onds), yo di se lineyè aplikasyon si tout konbinezon lineyè ak koyefisyan solisyon konstan se yon solisyon.
Pwopriyete sa a se karakteristik yon espas vektè kote chak pwen koresponn ak yon solisyon.
Yon seri solisyon diferan sèlman pa yon faktè pwopòsyonèl reyèl reprezante pa yon reyon, sa vle di yon liy ki pase nan orijin nan.
Nan akoustik, nan optik ak nan elektwomayetik yo rele yon reyon konsa mòd.
Si nou ka defini ortogonalite solisyon ki fè pati de mòd, nou ka defini ortogonalite mòd yo.
Nan acoustique ak elektwomayetik, de solisyon ortogonal si sòm enèjis chak solisyon egal a enèji sòm solisyon yo.
Ekwasyon diferans lan nan yon vag ka mennen nan solisyon ki gen enèji diminye ak tan, oswa nan vag "konsèvatif", ki gen enèji pa depann de tan.
Nan dènye ka a, nou ka estandadize solisyon yo, pou egzanp, nan elektwomayetik, nou ka deklare ke yon mòd monochromatic koresponn ak yon vektè inite si enèji li se pwodwi konstan Planck la pa frekans f vag la. Lè sa a, nou jwenn yon ankadreman referans ortonormal pou espas mòd la.
Nou ka eseye absòbe yon vag, pou egzanp yon bri anmèdan.
Pou rezon sa a, nou ka itilize "absorbers aktif" ki gen ladann loudspeakers ak elektwonik jenere vag lokalman nan opozisyon faz ak vag la twoublan.
Men, jenere yon vag konplèks egzakteman se irealizabl, ak tou de eksperyans ak teyori montre ke nou ka sèlman diminye vag la anmèdan.
Erezman, nan acoustics, vag yo pa konsèvatif ak bri a mouri.
Men, ekwasyon Maxwell yo nan vakyòm gouvène onn elektwomayetik konsèvatif, konsa yon vag ki emèt pa yon atòm pa ka anile pa vag lòt atòm emèt; kòm yon rezilta, rete onn rezidyèl yo rele "zewo pwen jaden", paske yo egziste nan yon kò nwa nan 0 K.
Remake byen ke jaden elektwomayetik nan yon mòd bay sèlman depann de yon paramèt reyèl, ki rele anplitid, se konsa ke li enposib yo fè distenksyon ant yon jaden pwen zewo ak nenpòt lòt jaden.
Nòt ak referans
[modifye | modifye kòd]- ↑ « Jaden vektè ».
- ↑ [PDF]« Gradyan yon fonksyon », sur aalem.free.fr.
- ↑ [PDF]« Jaden eskalatè, jaden vektè ».
Bibliyografi
[modifye | modifye kòd]- Matematik adisyonèl pou itilize enjenyè elektrik ak telekominikasyon,
- Daniel Duverney, « Calcul diferansyèl ak entegral pou fizik », sur touteslesmaths.fr
- Analiz vektè,











